Time-reversible computational methods

As interest in inverse problems and their related applications continues to grow across a wide range of disciplines of science and engineering, the size and complexity of inverse problems of practical interest is also increasing, introducing new challenges and potential barriers to the solution of large-scale inverse problems of emergent interest. Engineering disciplines have developed a broad interest in the solution of time-dependent optimization and inverse problems, such as structural/topology optimization, non-destructive evaluation, material characterization, optimal control, and others. These interests have been driven by increasingly complex designs and geometries made possible by additive manufacturing (AM) technologies, and by an increasing volume of measurement data for structural systems, such as through structural health monitoring technologies with potential applications to digital twins.

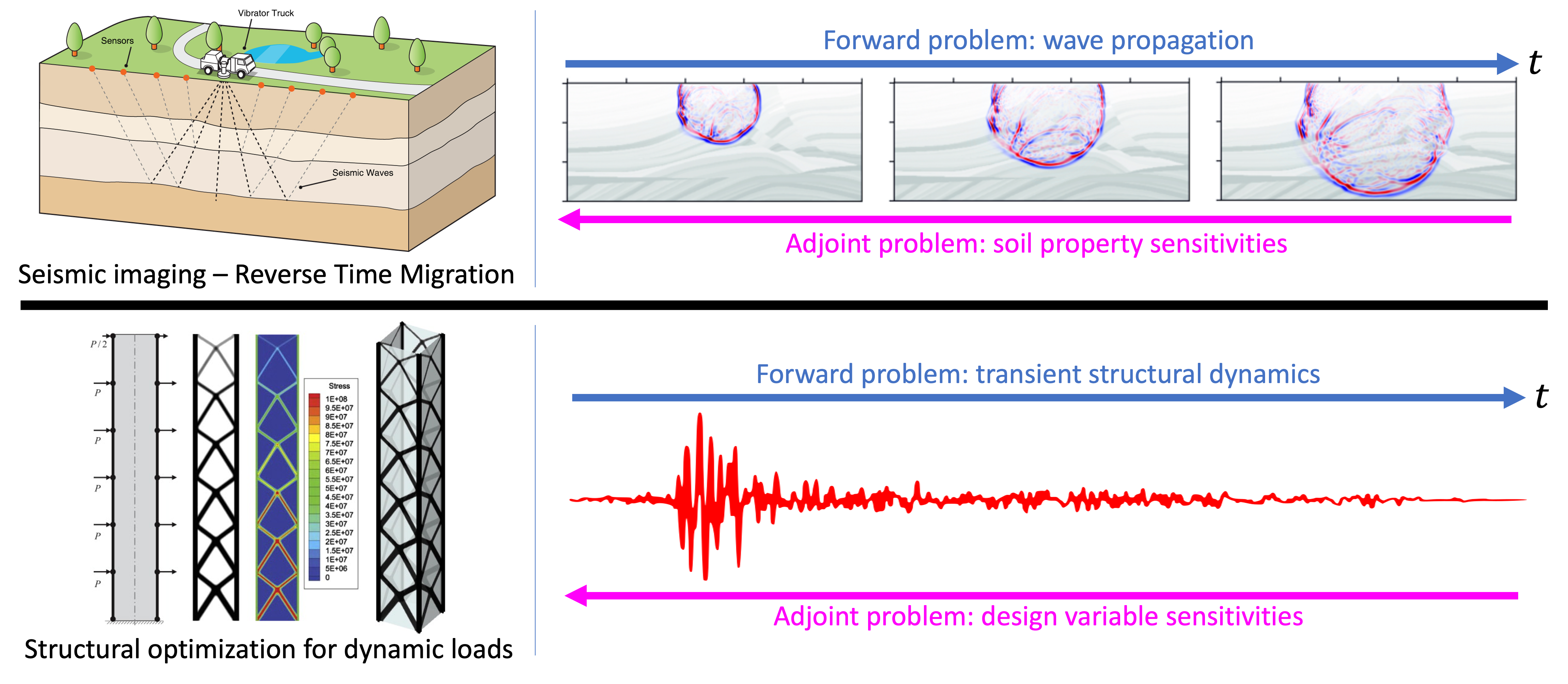
For optimization of time-dependent dynamic systems with a large number of optimization parameters, the adjoint state method is employed to compute the design parameter sensitivities within a gradient-based optimization framework, whereby the sensitivities for a given design iteration are computed by solving for a duplicate (adjoint) set of solution state variables which are evolved backwards in time from the final state of the computational analysis. Given that the adjoint state method requires the solution of the forward-in-time analysis to be known at all preceding time states, excessive memory or computational costs are incurred to either store or re-compute previous solution states, ultimately limiting the scalability and efficiency of the adjoint state method. These limitations become particularly onerous for computational methods using explicit time integrators that require a large number of time states to guarantee stability, requiring proportionately more data storage or computations as the number of time steps increases. Moreover, modern GPU-accelerated high-performance computing (HPC) architectures impose additional performance constraints: data communication bandwidth to/from the GPU tends to limit computational throughput, such that excessive memory transfers required by conventional adjoint state algorithms present a roadblock to GPU performance and scalability. To facilitate the solution of large-scale time-dependent optimization problems of emergent interest, and to leverage the full potential of modern and future computing technologies to efficiently accelerate their solution, there exists a critical need to develop fundamentally new algorithms and computational methods specifically designed to mitigate the high computational and data storage costs associated with conventional implementations of the adjoint state method.

The overarching goal of this ongoing research project is to identify novel computational methods enabling the efficient solution of large-scale inverse problems via adjoint state methods and reverse-mode differentiation. The primary goal is to explore and evaluate the feasibility and scalability of exactly time-reversible computational algorithms for the solution of large scale transient dynamic structural optimization problems by the adjoint state method. It is hypothesized that time-reversible methods applied to the computation of parameter sensitivities by the adjoint state method for the aforementioned class of problems are mathematically and computationally feasible, entail fewer computations, require less memory, and achieve improved scalability on GPU-enabled platforms compared to existing adjoint state approaches based on solution “checkpointing” schemes.

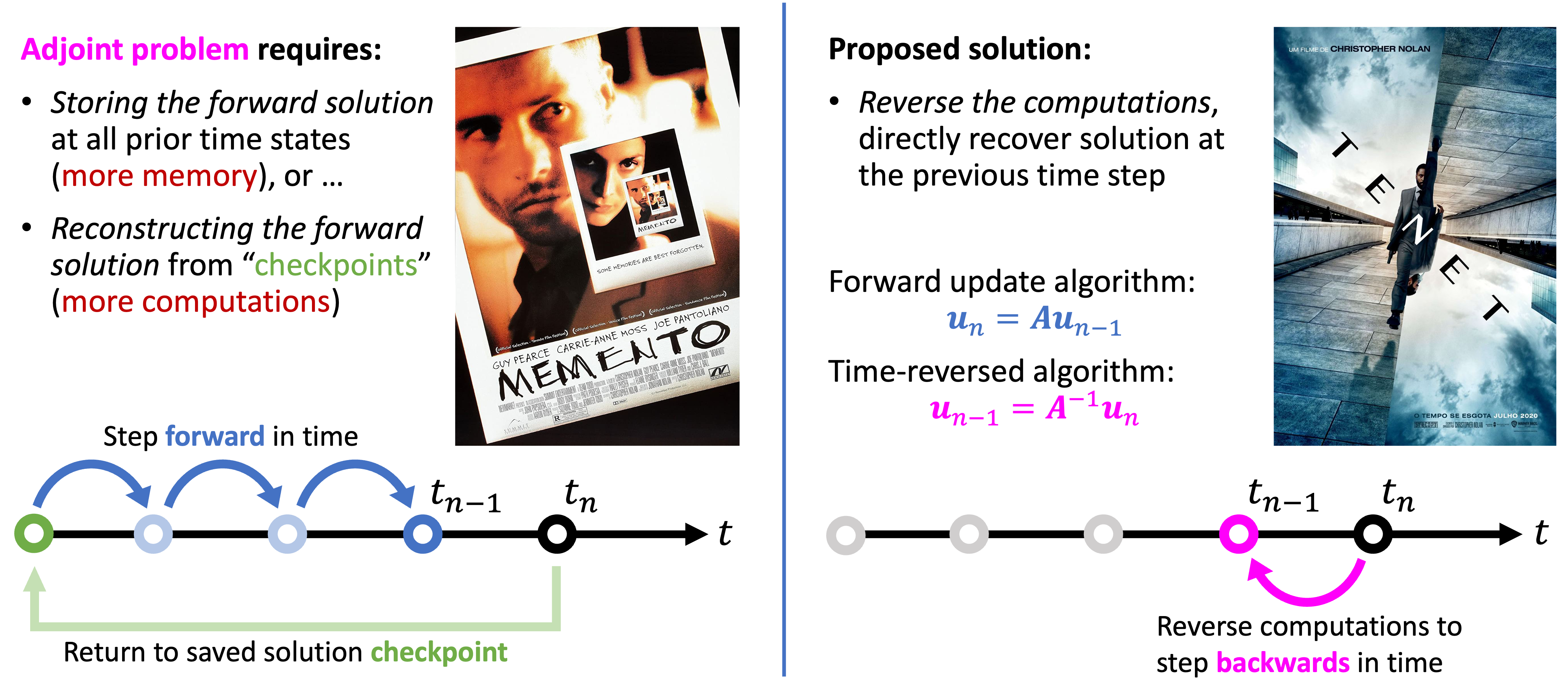
Intuitively, the relative differences between conventional checkpointing schemes and the proposed class of time-reversible methods for the solution of time-dependent inverse problems via the adjoint method can be understood through the following film-based analogy: in some respects, checkpointing shemes operate in a fashion which is similar to the Christopher Nolan film Memento. Without giving away the plot, the progression of events in Memento proceeds backwards in time by “skipping” back to an earlier moment in time, and then playing events forward in time up to the start of the previous scene in the film. By comparison, directly time-reversible methods bear similarities to another Christopher Nolan film: Tenet, in which the flow of time is directly reversed at various points throughout the film. While Memento is arguably the better film, Tenet nonetheless stands as the greater technological feat. The major difference being: Memento only ever play events forward in time, whereas Tenet plays events in reverse. In a similar manner, the potential benefits of developing simulation methods which can be directly reversed in time (ala Tenet) lies in the fact that we do not need to save previous solution checkpoints for the purpose of reconstructing prior solution states (ala Memento).