Hyper-dimensional contact gap methods
A novel finite element contact discretization method
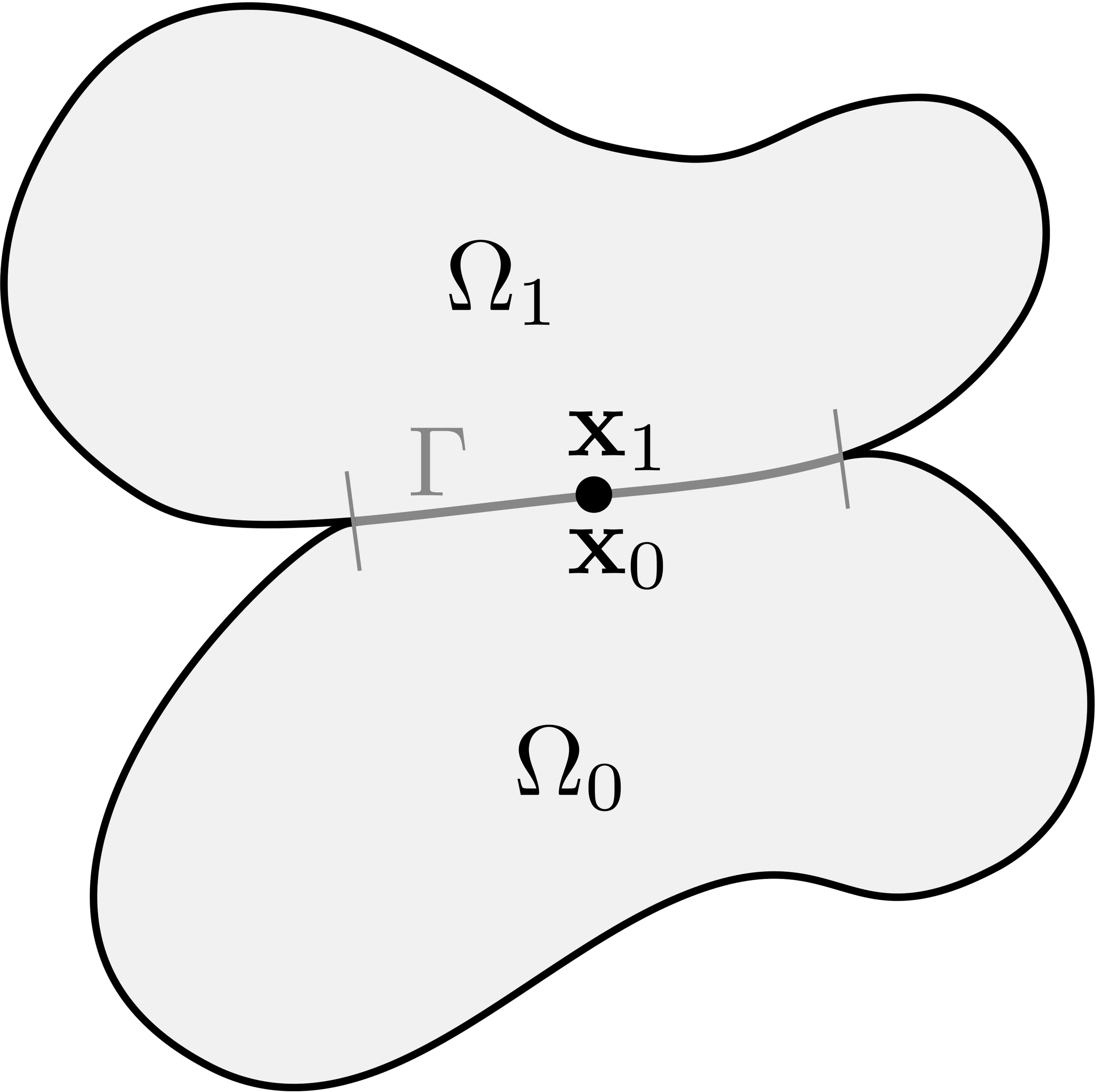
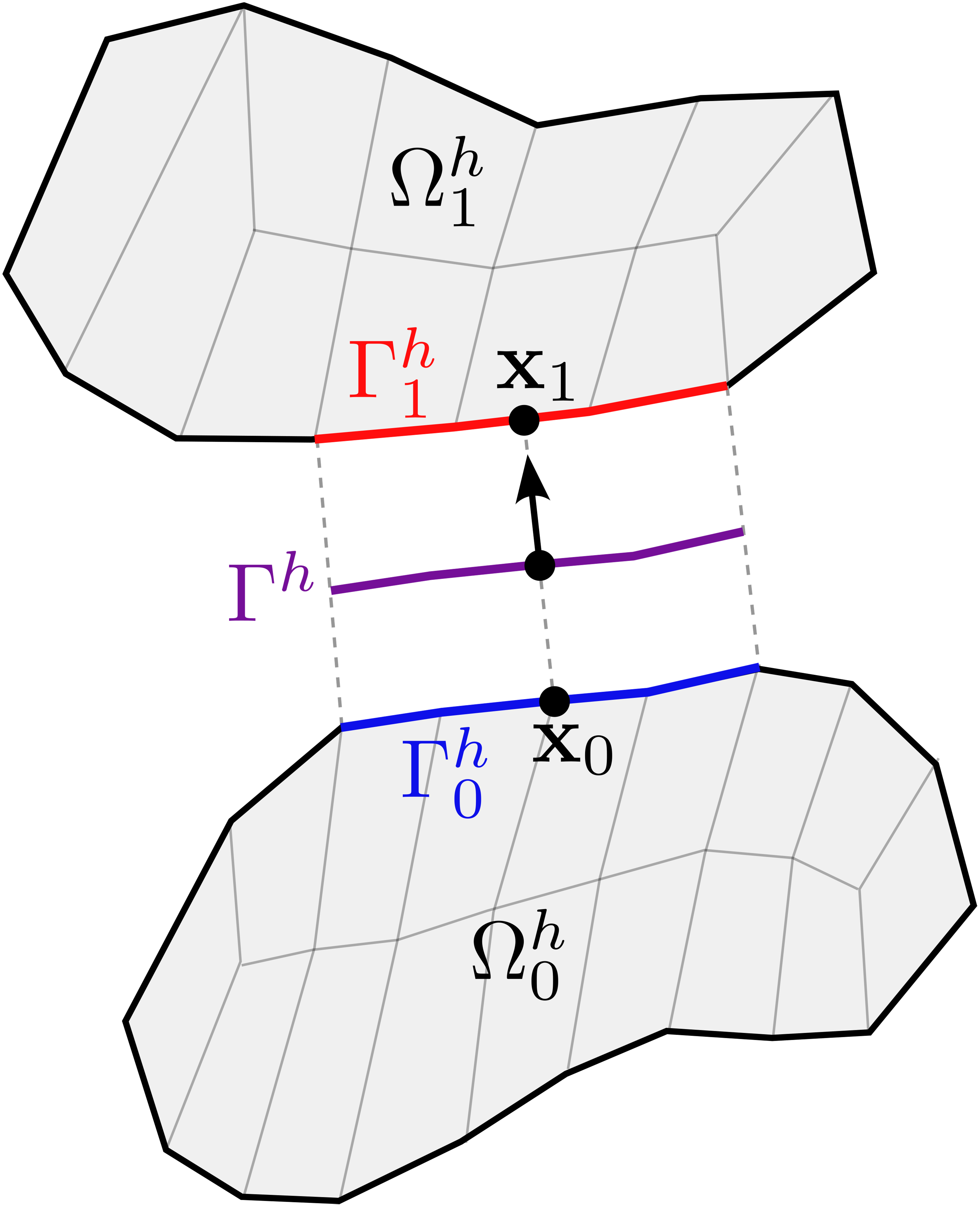
In the classical theory of two-body contact, a single shared contact interface is typically considered between two continuum bodies, and is further discretized as such in the finite element setting. In general, however, the finite element mesh topology of two contacting bodies will be non-conforming at this shared interface, requiring the definition of a preferred or intermediate surface over which integral constraints may be evaluated. The specification of this interface is deemed to be somewhat arbitrary, but in practice the numerical solution of contact problems may exhibit sensitivity to the particular choice of intermediate surface. A further complication concerns the need to establish projective mappings between the discretized finite element surfaces and the chosen intermediate surface, particularly for the sake of evaluating the contact gap function between pairs of points on each of the two bodies.

In general, the computational cost of numerically solving finite element problems involving contact may be attributed to the large number of iterations required to determine which regions of the contacting interface are “active,” which is compounded by the computational expense inherent to the algorithms used for proximity and overlap detection, geometric projection, and gap integral evaluation. Active efforts to reduce the computational expense of contact procedures has emphasized improvements in reducing cost associated with the non-linear iteration procedure, and with the computational geometry operations. The present contributions focus primarily on the latter.
The methodology proposed herein serves as a departure from classical finite element contact enforcement approaches, in that the restriction on conforming finite element surface topologies is relaxed. The manner in which the constraints are enforced, and how certain fundamental quantities of interest (gap, normal) are computed also differs from most other alternative contact discretization methods, and most closely resembles a “contact domain method.”


In this project (Giffin, 2024), a new methodology for the enforcement of contact constraints in the context of finite element analyses is proposed. The method entails an alternative representation of contact surface integrals by equivalently integrating over the interstitial – albeit degenerate gap volume between two contacting bodies. An auxiliary indicator field is defined on each body, and is used to represent the degenerate interstitial volume as a non-degenerate hyper-dimensional gap volume. Over this domain, the gradient of the continuously interpolated displacement field with respect to the indicator field yields the oriented displacement gap, which may be used in the formulation of contact inequality constraints. Discretization of the hyper-dimensional gap volume into conforming finite elements is explored, and is observed to offer several advantages over existing contact discretization methods: the proposed method does not require the computation of geometric intersections or projections; it exploits conventional Gaussian quadrature schemes to integrate the hyper-dimensional gap integrals with a sufficient degree of accuracy; and may be naturally and efficiently extended to represent contact between higher-order surfaces.
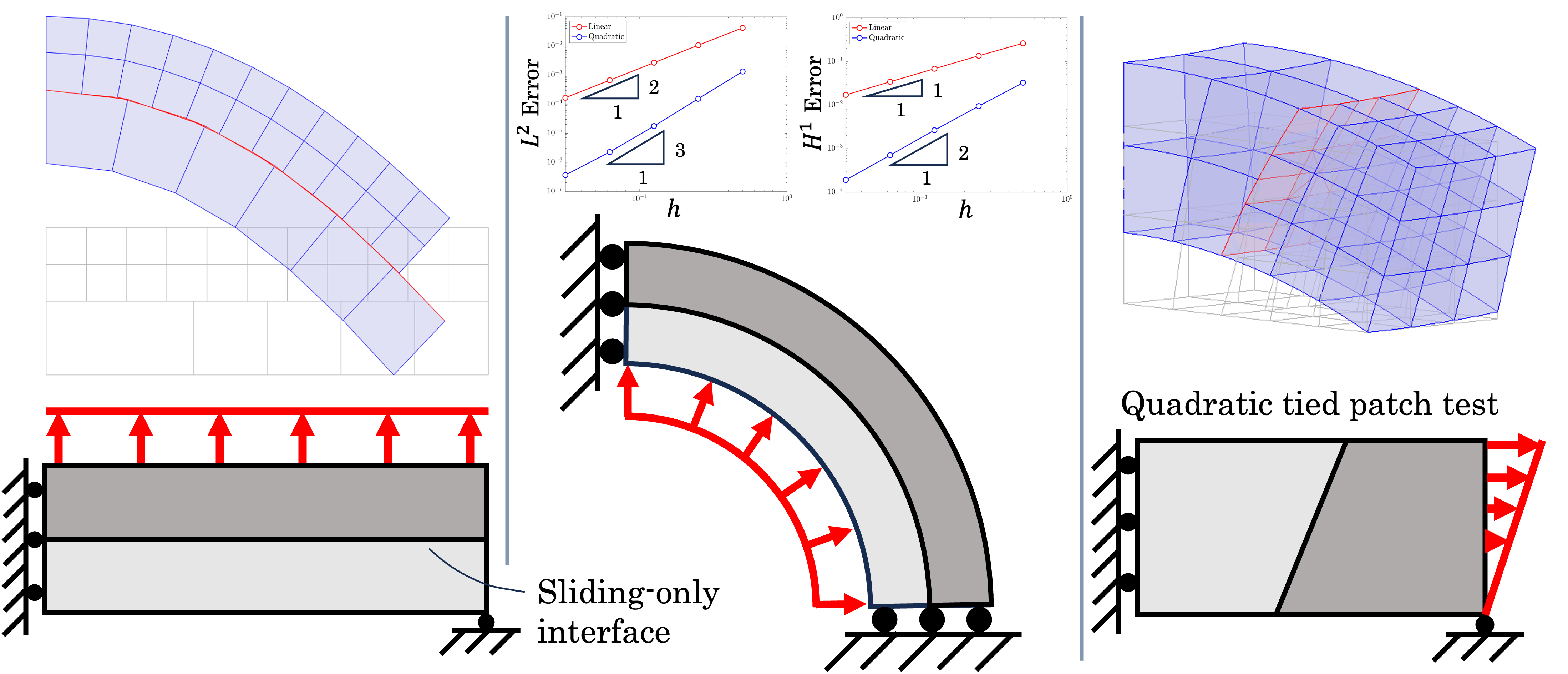
Initial investigations presented above verify that the proposed method achieves appropriate accuracy and rates of convergence for several benchmark problems. Ongoing work seeks to extend the proposed approach to accommodate more general contact constraints with frictional sliding and separation.